一、概述
学习此内容需一定计算几何基础,出门右拐:https://www.cnblogs.com/xzyxzy/p/10033130.html
官方定义:两个图形A,BA,B的闵可夫斯基和C=\{a+b|a\in A,b\in B\}C={a+b∣a∈A,b∈B}
通俗一点:从原点向图形A内部的每一个点做向量,将图形BB沿每个向量移动,所有的最终位置的并便是闵可夫斯基和
由于博主太菜,本文只讨论凸包的闵可夫斯基和
如下图,粉色区域便是三角形和一个不规则四边形的闵可夫斯基和?
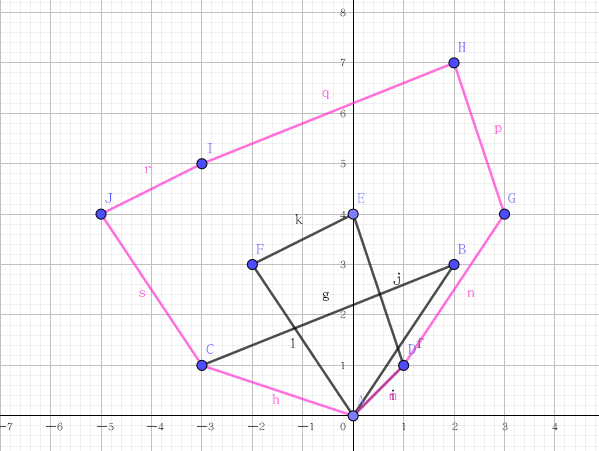
二、怎么求
利用瞪眼法得,闵可夫斯基和的边是由两凸包构成的
也就是说把两凸包的边极角排序后直接顺次连起来就是闵可夫斯基和
由于凸包的优美性质,直接归并排序就好了
但是需要注意的是可能会有三点共线的情况,于是再扔过去重新求一次凸包就好了
三、应用举例
题目
[JSOI2018]战争
两个凸包A,BA,B,移动BB,问是否还有交点。n\le10^5,q\le10^5n≤105,q≤105
正解
令a\in A,b\in Ba∈A,b∈B则移动向量ww使得存在b+w=ab+w=a
那么ww需要满足w=a-bw=a?b
构造闵可夫斯基和C=\{a+(-b)\}C={a+(?b)}
在输入BB的时候横纵坐标都取反即可
余下问题便是判断输入的移动向量是否在CC内,计算几何有讲
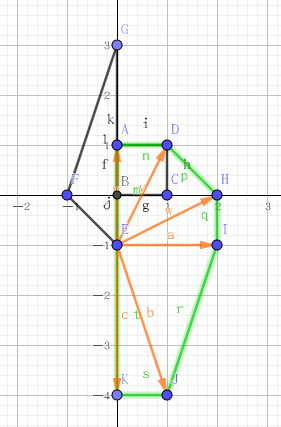
样例靓照
原图
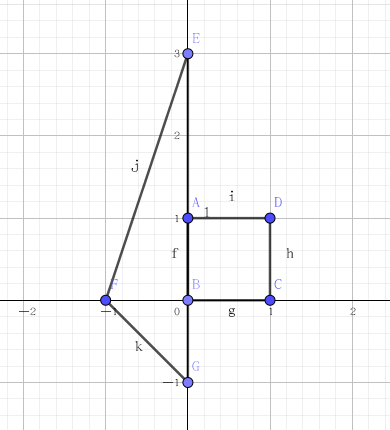
取反
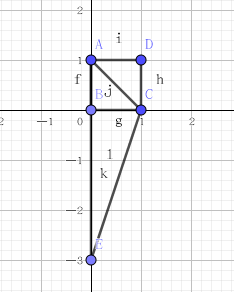
闵可夫斯基和
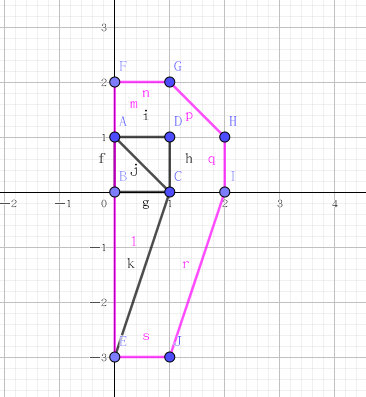
用题目意思去理解闵可夫斯基和:
橙色的向量是BB可以移动的范围的边界,也就是说在绿色框之内的向量都满足条件
这些向量拖到以原点为起点,就是上面的闵可夫斯基和的粉色区域
代码
我觉得这题值这个黑色标签
不是很好转换,有点策不清
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;
const ll N=1e5+10;
struct Node
{
ll x,y;
Node operator - (Node A) {return (Node){x-A.x,y-A.y};}
Node operator + (Node A) {return (Node){x+A.x,y+A.y};}
ll operator * (Node A) const {return x*A.y-y*A.x;}
ll len() const {return x*x+y*y;}
}A[N],C1[N],C2[N],s1[N],s2[N],bs;
ll cmp1(const Node&A,const Node&B) {return A.y<B.y||(A.y==B.y&&A.x<B.x);}
ll cmp2(const Node&A,const Node&B) {return A*B>0||(A*B==0&&A.len()<B.len());}
ll n,m,sta[N],top,q,tot;
void Convex(Node *A,ll &n)
{
sort(A+1,A+n+1,cmp1);
bs=A[1];sta[top=1]=1;
for(ll i=1;i<=n;i++) A[i]=A[i]-bs;
sort(A+2,A+n+1,cmp2);
for(ll i=2;i<=n;sta[++top]=i,i++)
while(top>=2&&(A[i]-A[sta[top-1]])*(A[sta[top]]-A[sta[top-1]])>=0) top--;
for(ll i=1;i<=top;i++) A[i]=A[sta[i]]+bs;
n=top;A[n+1]=A[1];
}
void Minkowski()
{
for(ll i=1;i<n;i++) s1[i]=C1[i+1]-C1[i];s1[n]=C1[1]-C1[n];
for(ll i=1;i<m;i++) s2[i]=C2[i+1]-C2[i];s2[m]=C2[1]-C2[m];
A[tot=1]=C1[1]+C2[1];
ll p1=1,p2=1;
while(p1<=n&&p2<=m) ++tot,A[tot]=A[tot-1]+(s1[p1]*s2[p2]>=0?s1[p1++]:s2[p2++]);
while(p1<=n) ++tot,A[tot]=A[tot-1]+s1[p1++];
while(p2<=m) ++tot,A[tot]=A[tot-1]+s2[p2++];
}
ll in(Node a)
{
if(a*A[1]>0||A[tot]*a>0) return 0;
ll ps=lower_bound(A+1,A+tot+1,a,cmp2)-A-1;
return (a-A[ps])*(A[ps%tot+1]-A[ps])<=0;
}
int main()
{
cin>>n>>m>>q;
for(ll i=1;i<=n;i++)
scanf("%lld%lld",&C1[i].x,&C1[i].y);
Convex(C1,n);
for(ll i=1;i<=m;i++)
{
scanf("%lld%lld",&C2[i].x,&C2[i].y);
C2[i].x=-C2[i].x;C2[i].y=-C2[i].y;
}
Convex(C2,m);
Minkowski();
Convex(A,tot);
bs=A[1];for(ll i=tot;i>=1;i--) A[i]=A[i]-A[1];
while(q--)
{
scanf("%lld%lld",&A[0].x,&A[0].y);
printf("%lld\n",in(A[0]-bs));
}
return 0;
}
cs






