转自http://blog.csdn.net/wangdingqiaoit/article/details/40405849
本节旨在对算法的复杂度度量有一个初步认识,形成一个清晰的思路。关于复杂度计算属于算法分析的范畴,在此处不做深入讨论。文章中引用的例子和定义所参考的教材,列在参考资料部分。
1.选择什么作为算法复杂度的度量标准?
???????? 作为算法运行复杂度度量标准,我们可能首先想到的是算法编程程序的运行时间。那么用运行时间作为算法复杂度是否合适呢?
????? 这种方式主要有一下几点弊端:
- ? 必须先运行依据算法编制的程序,然后才能统计时间
- ? 运行时间和具体系统相关。即是算法效率很低,但是如果利用“天河一号”超级计算机计算,也会比效率高的算法运行在普通PC上运行时间短。
- ?????????运行时间和编制程序的语言相关。即是利用同一台机器来运行程序,同一个程序,用C或者Ada编写就比用Basic或者Lisp编写快约20倍。更进一步,即是语言相同,语言的不同编译器实现,会产生不同质量的机器代码,这同样影响运行时间。
??????? 这说明,一个算法用不同的语言实现,或者用不同的编译程序进行编译,或者在不同的机器上运行,效率均不相同。而且有时候由于机器硬件、软件环境可能会掩盖算法本身的优劣。
????? 因此,使用绝对的时间单位作为衡量算法效率是不合适的。
?????我们应该采用某种逻辑单位,用它来描述问题规模n和运行时间t的关系,而且这种估算可以在运行程序之前进行。
?????问题的规模,一般可以认为是输入的长度,处理数据的个数等。例如运行时间可能与问题规模成线性关系,t=2n等。
????????? 通常,问题规模n与时间t的关系函数比较复杂,当数据量非常巨大时,我们没有必要计算出这个精确的值,转而使用近似值来代表这个算法的运行时间与问题规模之间的关系。这个近似值与原函数当数据量很大时,其实已经足够接近,我们就称这种估计方法为渐进复杂度。
?????????下面摘取自[1]的一个例子来帮助理解,为什么可以采用渐进复杂度来近似表达计算复杂度。
?????????假设f(n)为:
???????? 
????????? 则随着n的增长,我们得出如下的增长速度表(由office excel vba计算):
????????? 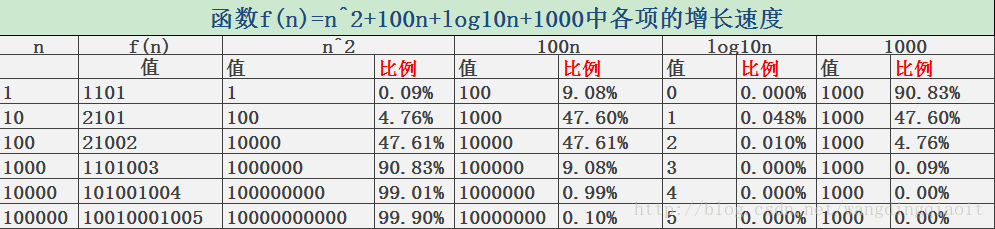
?????从这个表可以看出,当n=1,10时,100n和1000所占比重较大;当n=100时,n平方和100n所占比重相同;当n>100后,n平方所占比重越来越大,到最后n=100000时,n平方接近100%。这就说明,使用n平方来近似表达f(n)的计算复杂度是完全可行的。这里n平方一般表达为O(n^2),这种表达方式就是常用来表达渐进复杂度的大O记法,下面会详细介绍。
2.大O记法
??????定义1:?? 如果存在正数c和N,对于所有的n >= N,有f(n) <= cg(n),则f(n)=O(g(n))。
????? 大O记法的目的是表达问题规模函数f(n)的一个上界。例如刚才的f(n)=O(n^2)。
????????这里注意三点:
???????第一,对于一个函数f(n)<= cg(n),存在多个满足不等式的c和N,并且c的值决定了N的值,反过来也可以说N的值决定了c的值。
???????第二,这个定义表明,cg(n)几乎总是大于等于f,但是这是对于所有满足n >= N的n而言的。
?????? 第三,对于一个函数f(n)<= cg(n),也存在多个满足不等式的g(n),例如对于上面的f(n),我们可以取g(n)为n^3,n^4等等,为了避免这种情况,我们总是取最小的g函数,这称之为最小上界。
??????????实际上还存在几个类似定义:
???????? 1) 如果存在正数c和N,对于所有的n >= N,有f(n) >= cg(n),则f(n)=Ω(g(n))(读作Omega)。
???????????? 这是与大O对应的,表达f(n)的一个下界,即最大下界。
????? 2)如果存在正数c1,c2,和N,对于所有的n >= N,有c1g(n)<= f(n) <= c2g(n),则f(n)= Theta(g(n))。
???????? 还有小o等其他定义,在估计复杂度时,一般用得比较少,这里就不再给出定义。
??????????
???????? 关于大O记法,有许多性质,这里重点关注一点,就是O(logn)由来。
?????????????我们知道对数函数一般为logax,一定包含一个底a的。那么为什么使用logn?
????????首先我们给出一个性质1:??如果f(n) = cg(n),那么f(n)=O(g(n))。这是显然成立的。
?????????????下面摘取[1]的关于这一点的一个证明。
????????性质2:对于任意正数a,b(a,b>0,且a,b≠1),logan = O(logbn)。
????????????证明:?????? 令logan = x,logbn=y(1)则有:
??????????????????????????????????? ax= n,by =n??????? (2)
?????????????????????? 对(2)各个等式两边同时去ln,得到:
??????????????????????????????? 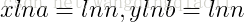 ?? (3)
?? (3)
?????????????????????????????????? 将(1)代入(3)式,得到:
??????????????????????????????????? 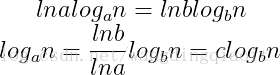 ???(4)
???(4)
???????????????????????????????? 由(4)及上述性质1即得到,logan = O(logbn)。
?????????? 这说明,对于对数而言,底数没有什么影响,因此可以取一个固定的底数,一般就取2作为底数,因此省略写成:O(logn)。
???????????对于n的函数,可以参考:Algorithmic Complexity and Big-O Notation,这里给出了一些常见函数的曲线图。
3.渐进复杂度计算的初步感受
???????????? 通常,我们选择一个对于所研究的问题来说是基本操作的原操作,以该操作重复执行的次数作为算法复杂度的时间度量。例如排序算法交换位置可以作为基本操作,查询算法中比较元素值是否相等可以作为基本操作。
????????????举两个简单的例子。
?????????????例子1:?
[cpp]
view plain
copycs



 ?? (3)
?? (3)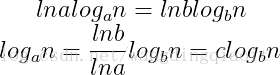 ???(4)
???(4)