目录
一,拟阵
1,拟阵
2,拟阵性质
3,独立子集的扩张
4,常见拟阵
5,图的拟阵
6,互补拟阵
二,加权拟阵
1,加权拟阵
2,最优子集
3,贪心问题的拟阵模型
4,求最优子集的通用算法
三,应用实例
单个处理器上对若干个单位时间任务的最优调度问题
一,拟阵
1,拟阵

换句话说,拟阵是一种满足遗传性和交换性的子集族。
2,拟阵性质
对于第二条,可以这么理解:
如果我们把I中不是I中其他任何元素的子集的元素,称为最大独立子集,那么最大独立子集的数量至少为1,而这些最大独立子集可以完全定义出I,
因为任意一个最大独立子集的所有子集都是I的元素,而且这些子集就包含了I的所有元素。
对于第三条,其实就是给这些最大独立子集加以限定。
首先,所有最大独立子集的元素个数都是一样的。
其次,第三条不仅仅是所有最大独立子集元素个数都一样这么简单,但是我没想出来怎么去表述。
3,独立子集的扩张
如果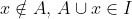 ,那么称x为A的扩张
,那么称x为A的扩张
4,常见拟阵
(1)S={1,2,3,4},I有9个元素{1,2}{1,3}{2,4}{3,4}{1}{2}{3}{4}{},其中{1,2}{1,3}{2,4}{3,4}是4个最大独立子集。
那么M=(S,I)就是一个简单的拟阵。
(2)S={1,2,3,4},I有11个元素{1,2}{1,3}{1,4}{2,3}{2,4}{3,4}{1}{2}{3}{4}{},其中{1,2}{1,3}{1,4}{2,3}{2,4}{3,4}是6个最大独立子集。
那么M=(S,I)就是一个简单的拟阵。
(3)显然(2)中的拟阵是非常简单的一种拟阵,可以直接推广:

(4)矩阵拟阵

(5)不那么显然的,(1)中的拟阵可以推广成:

5,图的拟阵

即S是一个图,它的所有无环边集构成一个拟阵。
根据图的性质很容易证明,这确实是拟阵,证明略。
对于一个全连通的图,最大独立子集就是生成树,元素个数就是 顶点数-1
6,互补拟阵

?
二,加权拟阵
1,加权拟阵
S中的每个元素都有一个权值,一个独立子集的权是它的所有元素的权之和

例如,图的拟阵中,权是边的长度,独立子集的权是所有包含的边的长度之和。
这里就得到了它和最小生成树的关系:对于一个全连通的图,如果每条边的权都大于0,那么权最小的最大独立子集就是最小生成树
2,最优子集
给定一个加权拟阵,所有元素的权都是正数,我们把具有最大权值的独立子集,称为最优子集。
因为所有元素的权值都是正数,所以最优子集一定是最大独立子集。
3,贪心问题的拟阵模型
很多贪心问题都可以转化成一个拟阵模型,即求最优子集。
例如求最小生成树,假设所以的边的权值都在(0,c)范围内,我们把所有边的权值乘以-1,再加上c,即从x变成c-x,
那么求最小生成树的问题,就转化成了求最大权值的最大独立子集,即求最优子集。
4,求最优子集的通用算法

算法非常简单,把所有元素按照权值递减排序,然后从头到尾扫描一遍,
独立子集A初始化为空集,扫描的过程中,如果A加上当前元素还是独立子集,那就加上,如果不是那就不加,
扫描完之后,就得到了最优子集。
实现:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef struct Node //需要根据实际修改
{
int w;
}Node;
#define N 100 //需要根据实际修改数值
Node s[N];
bool cmp(Node &a,Node &b)
{
return a.w>b.w;
}
template<typename T>
bool check(vector<T>&A)//判断是否是独立子集
{
return true; //需要根据实际修改逻辑
}
vector<Node> greedy()//求最优子集
{
vector<Node>A;
sort(s,s+N,cmp);
for(int i=0;i<N;i++){
A.push_back(s[i]);
if(!check(A))A.pop_back();
}
return A;
}
int main()
{
return 0;
}
其中,需要根据实际进行修改的有三处:规模N、结构体Node、判断是否是独立子集的函数check
时间复杂度:O(nlogn+nf(n)),其中f(n)是check函数运行的时间。
?
三,应用实例
单个处理器上对若干个单位时间任务的最优调度问题


思路:
首先,一个调度可以表示成早任务都在迟任务的前面的形式,早任务指的是能及时完成的任务。
其次,在早任务都在迟任务的前提下,一个调度可以表示成早任务全都是按照期限递增的形式。
所以,一个调度等价于一个早任务的集合。
那么,如何判断一个集合是不是独立集合呢?即如何实现check函数?

根据(2)即可完成check函数,时间复杂度为O(n)
所以整个算法的时间复杂度为O(n^2)
思路二:
如果不用拟阵,按照常规的贪心思路,把任务按照权值递减排序,然后从头到尾扫描,依次决定每个任务放到哪个位置,
如果当前还有时间槽可以完成这个任务,那就用其中最近(时间最靠后)的时间槽来完成这个任务,如果没有,那这个任务就是迟任务,不用调度了。
这个选时间槽的操作可以用并查集来完成:如还剩2个槽3,7,那么就有3棵树,根分别为0,3,7,成员分别是{0,1,2}{3,4,5,6}{7...},
这样就能根据任务的期限快速找出最近时间槽了。
?
?
cs


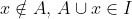 ,那么称x为A的扩张
,那么称x为A的扩张









