当前位置 博文首页 > liuchanglc：网络流最大流、最小割学习笔记
网络流 \(G=(V,E)\) 是一个有向图,其中每条边 \((u, v)\) 均有一个非负的容量值,记为 \(c(u, v)\geq0\)
如果 \((u, v)\notin E\),则可以规定 \(c(u, v)=0\)
网络流中有两个特殊的顶点,即源点 \(S\) 和汇点 \(T\) ,源点可以提供无限的流量,而汇点可以接受无限的流量
与网络流相关的一个概念是流
设 \(S\) 为网络的源点, \(T\) 为汇点，那么 \(G\) 的流是一个函数 \(f:V×V →R\),满足以下性质:
容量限制： \(\forall u,v∈V\)，满足 \(f(u, v) \leq c(u, v)\);
反对称性： \(\forall u,v∈V\)，满足 \(f(u, v) = - f(v, u)\);
流守恒性： \(\forall u∈V-{S, T}\)，满足\(\sum_{v∈V}f(u,v)=0\)。
流 \(f\) 的值定义为 \(|f|=\sum_{v\in V}f(s,v)\)
通俗地讲，我们想象一下自来水厂到你家的水管网是一个复杂的有向图，每一节水管都有一个最大承载流量。
自来水厂不放水，你家就断水了。
但是就算自来水厂拼命地往管网里面注水，你家收到的水流量也是上限，毕竟每根水管承载量有限。
你想知道你能够拿到多少水，这就是一种网络流问题。
以上摘自这篇博客
我们有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点），就是我们的最大流问题。
最大流的算法有很多，这里介绍的是 \(dinic\) 算法
算法的流程是从源点开始进行搜索，只要边权不为零就继续递归，直到到达汇点为止
在搜索的过程中记录当前路径上经过的最小边权，因为流量会受到最小边权的限制，回溯时把经过的边的边权都减去这个最小值
但是我们的选择不一定是最优的，所以对于每一条边，我们多建一条反向边
反向边的初始边权为 \(0\)
在正向边中减去的权值我们在反向边上加回来，相当于提供了一次反悔的机会
整个过程实际上就是寻找增广路的过程，当我们找不到增广路时算法就结束了
为了让算法更加高效，我们把图人为地进行分层
源点的深度为 \(1\)，从源点进行 \(bfs\)，更新能到达的每一个点的深度，把深度相同的点分到一层
在 \(dfs\) 寻找增广路时，我们规定只能从当前一层向下一层寻找，这样可以在一次递归中尽可能多得找出增广路
这就是 \(Dinic\) 算法的大体框架
时间复杂度为 \(O(n^2 m)\)，但是基本跑不满
为了让代码跑得更快，可以使用当前弧优化和无用点优化
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=2e5+5;
int h[maxn],h2[maxn],tot=2;
struct asd{
int to,nxt,val;
}b[maxn];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int q[maxn],dep[maxn],head,tail,n,m,s,t;
//bfs对原图进行分层
bool bfs(){
for(rg int i=1;i<=n;i++){
dep[i]=0;
h[i]=h2[i];
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(dep[u] || b[i].val==0) continue;
//如果已经访问过或者边权为0,continue
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
//如果不能到达汇点,返回0,否则返回1
return dep[t];
}
//dfs寻找增广路
long long dfs(int now,long long ac1){
if(now==t) return ac1;
rg long long ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
h[now]=i;
//优化一：当前弧优化，已经更新过并且边权变为0的节点下次不再访问
if(b[i].val && dep[u]==dep[now]+1){
rg long long nans=dfs(u,std::min(ac1,(long long)b[i].val));
b[i].val-=nans;
b[i^1].val+=nans;
ac2+=nans;
ac1-=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
//优化二：无用点优化，如果这个点不能对答案产生贡献下次不再访问
return ac2;
}
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read(),s=read(),t=read();
rg int aa,bb,cc;
for(rg int i=1;i<=m;i++){
aa=read(),bb=read(),cc=read();
ad(aa,bb,cc);
ad(bb,aa,0);
}
for(rg int i=1;i<=n;i++){
h2[i]=h[i];
}
rg long long ans=0;
while(bfs()){
ans+=dfs(s,1e18);
}
printf("%lld\n",ans);
return 0;
}
题目传送门
网络流的题难点还是在建图上
这道题用到了建图时的一个技巧：拆点
我们把一个石柱拆成两个点，一代表入口，另一个代表出口
首先，我们从超级源点向有蜥蜴的石柱的入口建一条边权为 \(1\) 的边，代表有一条蜥蜴可以经过这个石柱
然后，我们枚举所有的石柱，从当前石柱的出口向它能到达的所有石柱的入口建一条边权为无穷大的边
为了满足石柱高度的限制，我们还要从石柱的入口向自己的出口建一条边权为石柱高度的边，代表最多能从这里跳出的蜥蜴的个数
最后，我们再从所有石柱的出口向超级汇点连一条权值为无穷大的边
这道题拆点的目的就是为了便于处理石柱高度的限制
一个石柱跳的次数是有限的，如果我们不去拆点，这个限制是不好表示的
而我们把它人为地拆开之后，我们不需要去管它向外连了多少条边，我们只需要限制她经过这个石柱多少次就可以了
建完图后跑一次最大流，求出能逃走的蜥蜴最大数量
用蜥蜴的总数减去这个数量得到的就是答案
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5,maxm=1e6+5,maxk=25;
int h[maxn],tot=2,h2[maxn],n,m;
struct asd{
int to,nxt,val;
}b[maxm];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].val=cc;
b[tot].nxt=h[aa];
h[aa]=tot++;
}
char ss[maxk][maxk];
int a[maxk][maxk],dep[maxn],mmax,q[maxn],head,tail,s,t,d,totcnt;
bool bfs(){
for(rg int i=0;i<=mmax;i++){
h[i]=h2[i];
dep[i]=0;
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && b[i].val){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
int dfs(int now,int ac1){
if(now==t) return ac1;
rg int ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
h[now]=i;
if(dep[u]==dep[now]+1 && b[i].val){
rg int nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
return ac2;
}
int js(int i,int j){
return (i-1)*m+j;
}
double jl(int ax,int ay,int bx,int by){
return (double)sqrt((ax-bx)*(ax-bx)+(ay-by)*(ay-by));
}
bool pd(int i,int j){
if(i<=d || j<=d) return 1;
if(i+d>n || j+d>m) return 1;
return 0;
}
int main(){
n=read(),m=read(),d=read();
memset(h,-1,sizeof(h));
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
scanf("%1d",&a[i][j]);
}
}
for(rg int i=1;i<=n;i++){
scanf("%s",ss[i]+1);
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(ss[i][j]=='L'){
totcnt++;
ad(0,js(i,j),1);
ad(js(i,j),0,0);
}
if(a[i][j]!=0){
ad(js(i,j),js(i,j)+n*m,a[i][j]);
ad(js(i,j)+n*m,js(i,j),0);
for(rg int o=1;o<=n;o++){
for(rg int p=1;p<=m;p++){
if(a[o][p]!=0 && jl(i,j,o,p)<=(double)d && (o!=i || p!=j)){
ad(js(i,j)+n*m,js(o,p),0x3f3f3f3f);
ad(js(o,p),js(i,j)+n*m,0);
}
}
}
}
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(a[i][j]!=0 && pd(i,j)){
ad(js(i,j)+n*m,n*m*2+1,0x3f3f3f3f);
ad(n*m*2+1,js(i,j)+n*m,0);
}
}
}
s=0,t=n*m*2+1;
mmax=n*m*2+1;
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
rg int ans=0;
while(bfs()) ans+=dfs(s,0x3f3f3f3f);
printf("%d\n",totcnt-ans);
return 0;
}
题目传送门
我们知道的只是单位时间内激光武器对装甲的伤害
时间不确定，伤害就不确定，也就无法建图
所以我们二分时间，把这个问题转化为一个判定性问题
具体的建图就很简单了
\(1\)、从源点向所有激光武器建一条权值为激光武器总伤害的边
\(2\)、从激光武器向所有它能攻击的机器人建一条权值为 \(inf\) 的边
\(3\)、从机器人向汇点建一条权值为机器人装甲值的边
判断最大流是不是装甲值之和即可
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
typedef double db;
const db eps=1e-8;
const int maxn=105,maxm=1e4+5;
int h[maxn],tot=2;
struct asd{
int to,nxt;
db val;
}b[maxm];
void ad(int aa,int bb,db cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int jla[maxn],jlb[maxn],a[maxn][maxn],n,m,s,t,mmax,h2[maxn];
db sum;
int dep[maxn],q[maxn],head,tail;
db dfs(int now,db ac1){
if(now==t) return ac1;
db ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
h[now]=i;
rg int u=b[i].to;
if(std::fabs(b[i].val)>eps && dep[u]==dep[now]+1){
rg db nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(std::fabs(ac1)<eps) break;
}
if(std::fabs(ac2)<eps) dep[now]=0;
return ac2;
}
bool bfs(){
for(rg int i=0;i<=mmax;i++){
h[i]=h2[i];
dep[i]=0;
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && std::fabs(b[i].val)>eps){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
db dinic(){
rg db nans=0;
while(bfs()){
nans+=dfs(s,1e9);
}
return nans;
}
bool jud(db val){
memset(h,-1,sizeof(h));
tot=2;
for(rg int i=1;i<=m;i++){
ad(s,i,(db)jlb[i]*val);
ad(i,s,0);
}
for(rg int i=1;i<=m;i++){
for(rg int j=1;j<=n;j++){
if(a[i][j]){
ad(i,j+m,1e9);
ad(j+m,i,0);
}
}
}
for(rg int i=1;i<=n;i++){
ad(i+m,t,(db)jla[i]);
ad(t,i+m,0);
}
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
return dinic()>=sum;
}
int main(){
n=read(),m=read();
for(rg int i=1;i<=n;i++){
jla[i]=read();
sum+=jla[i];
}
for(rg int i=1;i<=m;i++){
jlb[i]=read();
}
for(rg int i=1;i<=m;i++){
for(rg int j=1;j<=n;j++){
a[i][j]=read();
}
}
s=0,t=n+m+1,mmax=n+m+1;
db l=0,r=1e9,mids;
while(r-l>eps){
mids=(l+r)/2.0;
if(jud(mids)) r=mids;
else l=mids;
}
printf("%.6f\n",mids);
return 0;
}
题目传送门
不是很好想
看到二维棋盘上的问题考虑黑白染色
设一共有 \(cnt1\) 个白点，这些白点的权值和为 \(sum1\)
设一共有 \(cnt2\) 个黑点，这些黑点的权值和为 \(sum2\)
因为我们每一次会对相邻的格子操作
也就是说操作若干次后，黑点和白点增加的总价值是相同的
设最后棋盘上的点都变成了 \(x\)
那么就有 \(x \times cnt1-sum1=x \times cnt2 -sum2\)
化简后可得 \(x(cnt1-cnt2)=sum1-sum2\)
此时，如果 \(cnt1-cnt2\) 不为 \(0\)
那么我们就可以这一部分除过去得到 \(x\) 的值判断是否合法即可
如果为 \(0\)，那么说明棋盘内格子的总个数一定为偶数
如果 \(x\) 合法，一定可以经过若干次操作后变成 \(x+1\)
所以可以二分答案然后判断是否合法
判断是否合法可以跑网络流
设棋盘中原来的数为 \(val\)
\(1\)、从源点向所有白点建一条权值为 \(x-val\) 的边
\(2\)、从白点向所有和它相邻的黑点建一条权值为 \(inf\) 的边
\(3\)、从黑点向汇点建一条权值为 \(x-val\) 的边
判断最大流是否等于 \(\sum(x-val)\) 即可
注意二分的下界要从原图的最大权值开始选
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=2e3+5,maxm=2e4+5;
const int dx[6]={0,0,-1,1},dy[6]={-1,1,0,0};
const long long INF=100000000000000LL;
int h[maxn],tot=2,n,m,tt;
struct asd{
int to,nxt;
long long val;
}b[maxm];
void ad(int aa,int bb,long long cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int js(int i,int j){
return (i-1)*m+j;
}
int a[maxn][maxn],s,t,h2[maxn],mmax,cnt0,cnt1,jlmax;
bool jud[maxn][maxn];
long long sum0,sum1;
int dep[maxn],q[maxn],head,tail;
bool bfs(){
for(rg int i=0;i<=mmax;i++){
dep[i]=0;
h[i]=h2[i];
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && b[i].val){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
long long dfs(int now,long long ac1){
if(now==t) return ac1;
long long ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
h[now]=i;
rg int u=b[i].to;
if(dep[u]==dep[now]+1 && b[i].val){
rg long long nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
return ac2;
}
bool pd(long long val){
memset(h,-1,sizeof(h));
tot=2;
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(jud[i][j]==0){
ad(s,js(i,j),std::max(val-a[i][j],0LL));
ad(js(i,j),s,0);
} else {
ad(js(i,j),t,std::max(val-a[i][j],0LL));
ad(t,js(i,j),0);
}
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(jud[i][j]) continue;
for(rg int k=0;k<4;k++){
rg int nx=i+dx[k],ny=j+dy[k];
if(nx<1 || ny<1 || nx>n || ny>m || jud[nx][ny]==jud[i][j]) continue;
ad(js(i,j),js(nx,ny),INF);
ad(js(nx,ny),js(i,j),0);
}
}
}
rg long long nans=0,mans=0;
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(jud[i][j]==0) mans+=std::max(val-a[i][j],0LL);
}
}
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
while(bfs()){
nans+=dfs(s,INF);
}
if(nans==mans) return 1;
else return 0;
}
int main(){
tt=read();
while(tt--){
sum0=sum1=0,cnt0=cnt1=jlmax=0;
n=read(),m=read();
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
a[i][j]=read();
jlmax=std::max(jlmax,a[i][j]);
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(j==1){
jud[i][j]=jud[i-1][j]^1;
} else {
jud[i][j]=jud[i][j-1]^1;
}
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(jud[i][j]){
cnt1++;
sum1+=a[i][j];
} else {
cnt0++;
sum0+=a[i][j];
}
}
}
s=0,t=n*m+1,mmax=n*m+1;
if(cnt0!=cnt1){
rg long long now=1LL*(sum1-sum0)/(cnt1-cnt0);
if(pd(now) && now>=jlmax) printf("%lld\n",1LL*now*cnt0-sum0);
else printf("-1\n");
} else {
rg long long l=jlmax,r=INF,mids;
while(l<=r){
mids=(l+r)>>1;
if(pd(mids)) r=mids-1;
else l=mids+1;
}
if(pd(l)==0) printf("-1\n");
else printf("%lld\n",1LL*cnt0*l-sum0);
}
}
return 0;
}
题目传送门
逆向思维
考虑一开始把所有的格子都放上士兵，求出最多能够删掉多少士兵即可
分别计算每一行每一列最多有多少格子可以放士兵，设为 \(cnt1,cnt2\)
\(1\)、从源点向代表第 \(i\) 行的点建一条权值为 \(cnt1[i]-L[i]\) 的边
代表这一行最多可以被删多少士兵
\(2\)、如果 \((i,j)\) 位置可以放士兵，那么从代表第 \(i\) 行的点向代表第 \(j\) 列的点建一条权值为 \(1\) 的点，代表这个点可以不放士兵
\(3\)、从代表第 \(j\) 列的点向汇点建一条权值为 \(cnt2[j]-L[j]\) 的边
代表这一列最多可以被删多少士兵
答案就是总的士兵数减去最大流
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e3+5,maxm=1e6+5;
int h[maxn],tot=2,n,m,l[maxn],c[maxn],k,h2[maxn],cnt1[maxn],cnt2[maxn],a[maxn][maxn],s,t,mmax;
struct asd{
int to,nxt,val;
}b[maxm];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int dep[maxn],q[maxn],head,tail;
bool bfs(){
for(rg int i=0;i<=mmax;i++){
dep[i]=0;
h[i]=h2[i];
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && b[i].val){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
int dfs(int now,int ac1){
if(now==t) return ac1;
int ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
h[now]=i;
rg int u=b[i].to;
if(dep[u]==dep[now]+1 && b[i].val){
rg int nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
return ac2;
}
int main(){
memset(h,-1,sizeof(h));
m=read(),n=read(),k=read();
for(rg int i=1;i<=m;i++){
l[i]=read();
cnt1[i]=n;
}
for(rg int i=1;i<=n;i++){
c[i]=read();
cnt2[i]=m;
}
rg int aa,bb;
for(rg int i=1;i<=k;i++){
aa=read(),bb=read();
a[aa][bb]=1;
cnt1[aa]--;
cnt2[bb]--;
}
for(rg int i=1;i<=m;i++){
if(cnt1[i]<l[i]){
printf("JIONG!\n");
return 0;
}
cnt1[i]-=l[i];
}
for(rg int i=1;i<=n;i++){
if(cnt2[i]<c[i]){
printf("JIONG!\n");
return 0;
}
cnt2[i]-=c[i];
}
s=0,t=n+m+1,mmax=n+m+1;
for(rg int i=1;i<=m;i++){
ad(s,i,cnt1[i]);
ad(i,s,0);
}
for(rg int i=1;i<=n;i++){
ad(i+m,t,cnt2[i]);
ad(t,i+m,0);
}
for(rg int i=1;i<=m;i++){
for(rg int j=1;j<=n;j++){
if(a[i][j]!=1){
ad(i,j+m,1);
ad(j+m,i,0);
}
}
}
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
rg int nans=0;
while(bfs()){
nans+=dfs(s,100000000);
}
nans=n*m-k-nans;
printf("%d\n",nans);
return 0;
}
将选中的边删去之后, \(s\) 和 \(t\) 不再连通, 点集 \(V\) 被分割为两部分 \(V_s\) 和 \(V_t\) . 我们称点集 \((V_s,V_t)\) 为流网络的一个割, 定义它的容量为所有满足 \(u\in V_s, v\in V_t\) 的边 \((u,v)\) 的容量之和
可以理解为找一些边满足从 \(s\) 到 \(t\) 的任意路径都必须至少经过一条这些边, 同时让这些选中的边的权值最小.
最大流最小割定量： 在任何的网络中，最大流的值等于最小割的容量。
题目传送门
一个最小割的板子题，把图建出来之后直接跑一个最小割就行了
但是时间复杂度比较玄学
一种更优秀的做法是对原图建一个对偶图，然后跑最短路
引用 Imakf博客 的图可能更好理解一些
大概就是把割边的花费变成了边权
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=2e6+5,maxm=3e6+5;
int h[maxn],tot=2,n,m,h2[maxn],s,t,mmax;
struct asd{
int to,nxt,val;
}b[maxm<<1];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int dis[maxn];
bool vis[maxn];
struct jie{
int num,dis;
jie(){}
jie(int aa,int bb){
num=aa,dis=bb;
}
bool operator < (const jie& A)const{
return dis>A.dis;
}
};
std::priority_queue<jie> q;
void dij(){
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
q.push(jie(s,0));
while(!q.empty()){
rg int now=q.top().num;
q.pop();
if(vis[now]) continue;
vis[now]=1;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(dis[u]>dis[now]+b[i].val){
dis[u]=dis[now]+b[i].val;
q.push(jie(u,dis[u]));
}
}
}
}
int js(int i,int j){
return (i-1)*(m-1)+j;
}
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read();
rg int aa,nans=0x3f3f3f3f;
if(n==1 || m==1){
rg int d=(n==1)?m:n;
for(rg int i=1;i<d;i++){
aa=read();
nans=std::min(nans,aa);
}
printf("%d\n",nans);
return 0;
}
s=0,t=n*m+1;
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<m;j++){
aa=read();
if(i==1){
ad(s,js(i,j),aa);
ad(js(i,j),s,aa);
} else if(i==n){
ad(js(i*2-2,j),t,aa);
ad(t,js(i*2-2,j),aa);
} else {
ad(js(i*2-2,j),js(i*2-1,j),aa);
ad(js(i*2-1,j),js(i*2-2,j),aa);
}
}
}
for(rg int i=1;i<n;i++){
for(rg int j=1;j<=m;j++){
aa=read();
if(j==1){
ad(js(i*2,j),t,aa);
ad(t,js(i*2,j),aa);
} else if(j==m){
ad(s,js(i*2-1,m-1),aa);
ad(js(i*2-1,m-1),s,aa);
} else {
ad(js(i*2-1,j-1),js(i*2,j),aa);
ad(js(i*2,j),js(i*2-1,j-1),aa);
}
}
}
for(rg int i=1;i<n;i++){
for(rg int j=1;j<m;j++){
aa=read();
ad(js(i*2-1,j),js(i*2,j),aa);
ad(js(i*2,j),js(i*2-1,j),aa);
}
}
dij();
printf("%d\n",dis[t]);
return 0;
}
题目传送门
把割点看成割边，新建一个虚拟层 \(R+1\)，实际上就是求一个最小割
先不考虑光滑程度的限制
由源点向第一层中所有的点建一条边权为 \(inf\) 的边，由第 \(R+1\) 层中所有的点向汇点建一条边权为 \(inf\) 的边，这些边都是割不掉的
然后对于任何一个 \(1\leq i\leq P,1\leq j\leq Q,1\leq k\leq R\)，由 \((i,j,k)\) 向 \((i,j,k+1)\) 连一条容量为 \((i,j,k)\)的不和谐值的边
对于光滑程度的限制 \(d\)
由 \((i,j,k)\) 向 \((i \pm 1,j,k?d)\) 和 \((i,j\pm 1,k-d)\) 建边权为 \(inf\) 的边就可以了
这样如果割两个高度差大于 \(d\) 的边，就还会有一条 \(inf\) 的通路，使得 \(S,T\) 连通。
限制了不能割这样的两条边。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5,maxm=45;
const int dx[6]={0,0,1,-1},dy[6]={1,-1,0,0};
int h[maxn],tot=2,n,m,r,d,h2[maxn],s,t,mmax,a[maxm][maxm][maxm];
struct asd{
int to,nxt,val;
}b[maxn<<1];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int dep[maxn],q[maxn],head,tail;
bool bfs(){
for(rg int i=0;i<=mmax;i++){
dep[i]=0;
h[i]=h2[i];
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && b[i].val){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
int dfs(int now,int ac1){
if(now==t) return ac1;
int ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
h[now]=i;
rg int u=b[i].to;
if(dep[u]==dep[now]+1 && b[i].val){
rg int nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
return ac2;
}
int js(int i,int j,int k){
return (k-1)*n*m+(i-1)*m+j;
}
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read(),r=read(),d=read();
for(rg int k=1;k<=r;k++){
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
a[i][j][k]=read();
}
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
for(rg int k=1;k<=r;k++){
ad(js(i,j,k),js(i,j,k+1),a[i][j][k]);
ad(js(i,j,k+1),js(i,j,k),0);
}
}
}
s=0,t=n*m*(r+1)+1,mmax=n*m*(r+1)+1;
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
ad(s,js(i,j,1),0x3f3f3f3f);
ad(js(i,j,1),s,0);
ad(js(i,j,r+1),t,0x3f3f3f3f);
ad(t,js(i,j,r+1),0);
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
for(rg int k=d+1;k<=r+1;k++){
for(rg int o=0;o<4;o++){
rg int nx=i+dx[o],ny=j+dy[o];
if(nx<1 || nx>n || ny<1 || ny>m) continue;
ad(js(i,j,k),js(nx,ny,k-d),0x3f3f3f3f);
ad(js(nx,ny,k-d),js(i,j,k),0);
}
}
}
}
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
rg int nans=0;
while(bfs()){
nans+=dfs(s,0x3f3f3f3f);
}
printf("%d\n",nans);
return 0;
}
题目传送门
经典的最大权闭合子图问题
\(1\)、由源点向所有的用户建边权为收益的边
\(2\)、由用户向基站建边权为 \(inf\) 的边
\(3\)、由基站向汇点建边权为花费的边
答案就是总收益减去最小割
可以这样理解
如果我们割掉了用户，就代表我们放弃这个用户的收益
如果我们割掉了基站，就代表我们要建造这个基站，这要有一定的花费
用户和基站之间建边权为 \(inf\) 的边实际上是一种强制关系
这些边是割不掉的，如果我们选择了用户，那么必须建造相应的基站
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5,maxm=3e6+5;
int h[maxn],tot=2,n,m,h2[maxn],s,t,mmax,a[maxn];
struct asd{
int to,nxt,val;
}b[maxm<<1];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int dep[maxn],q[maxn],head,tail;
bool bfs(){
for(rg int i=0;i<=mmax;i++){
dep[i]=0;
h[i]=h2[i];
}
q[head=tail=1]=s;
dep[s]=1;
while(head<=tail){
rg int now=q[head++];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!dep[u] && b[i].val){
dep[u]=dep[now]+1;
q[++tail]=u;
}
}
}
return dep[t];
}
int dfs(int now,int ac1){
if(now==t) return ac1;
int ac2=0;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
h[now]=i;
rg int u=b[i].to;
if(dep[u]==dep[now]+1 && b[i].val){
rg int nans=dfs(u,std::min(ac1,b[i].val));
ac1-=nans;
ac2+=nans;
b[i].val-=nans;
b[i^1].val+=nans;
}
if(ac1==0) break;
}
if(ac2==0) dep[now]=0;
return ac2;
}
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read();
s=0,t=n+m+1,mmax=n+m+1;
rg int ans=0;
for(rg int i=1;i<=n;i++){
a[i]=read();
ad(i+m,t,a[i]);
ad(t,i+m,0);
}
rg int aa,bb,cc;
for(rg int i=1;i<=m;i++){
aa=read(),bb=read(),cc=read();
ad(i,aa+m,0x3f3f3f3f);
ad(aa+m,i,0);
ad(i,bb+m,0x3f3f3f3f);
ad(bb+m,i,0);
ad(s,i,cc);
ad(i,s,0);
ans+=cc;
}
for(rg int i=0;i<=mmax;i++){
h2[i]=h[i];
}
rg int nans=0;
while(bfs()){
nans+=dfs(s,0x3f3f3f3f);
}
printf("%d\n",ans-nans);
return 0;
}
题目传送门
和上一道题一样，用总价值减去图中的最小割
问题在于如何建边
首先由 \(s\) 向 \((i,j)\) 建边，边权为选文的价值
由 \((i,j)\) 向 \(t\) 建边，边权为选理的价值
先处理同选文的限制
对于\((i,j)\) 和 \((i+1,j)\) 两个点的组合情况
假设这两个点同时选文科有 \(w\) 的喜悦值
新建一个节点 \(x\)，从 \(s\) 向 \(x\) 连一条容量为喜悦值 \(w\) 的边
再从 \(x\) 向 \((i,j)\) 和 \((i+1,j)\) 分别连一条容量为 \(inf\) 的边
其它情况同理
考虑这样做为什么是正确的
如果 \(a\) 和 \(b\) 中有一个没有选文，那么必定一条选理的边没有被割掉
\(s \to x \to a/b \to t\) 这条路径仍然是联通的，原图并没有被割掉
\(x \to a\) 的边权是 \(inf\) ,肯定割不掉
所以我们只能割掉 \(s \to x\) 这条边
也就是说恰好把同选文的贡献割掉了
还有一种解方程的做法
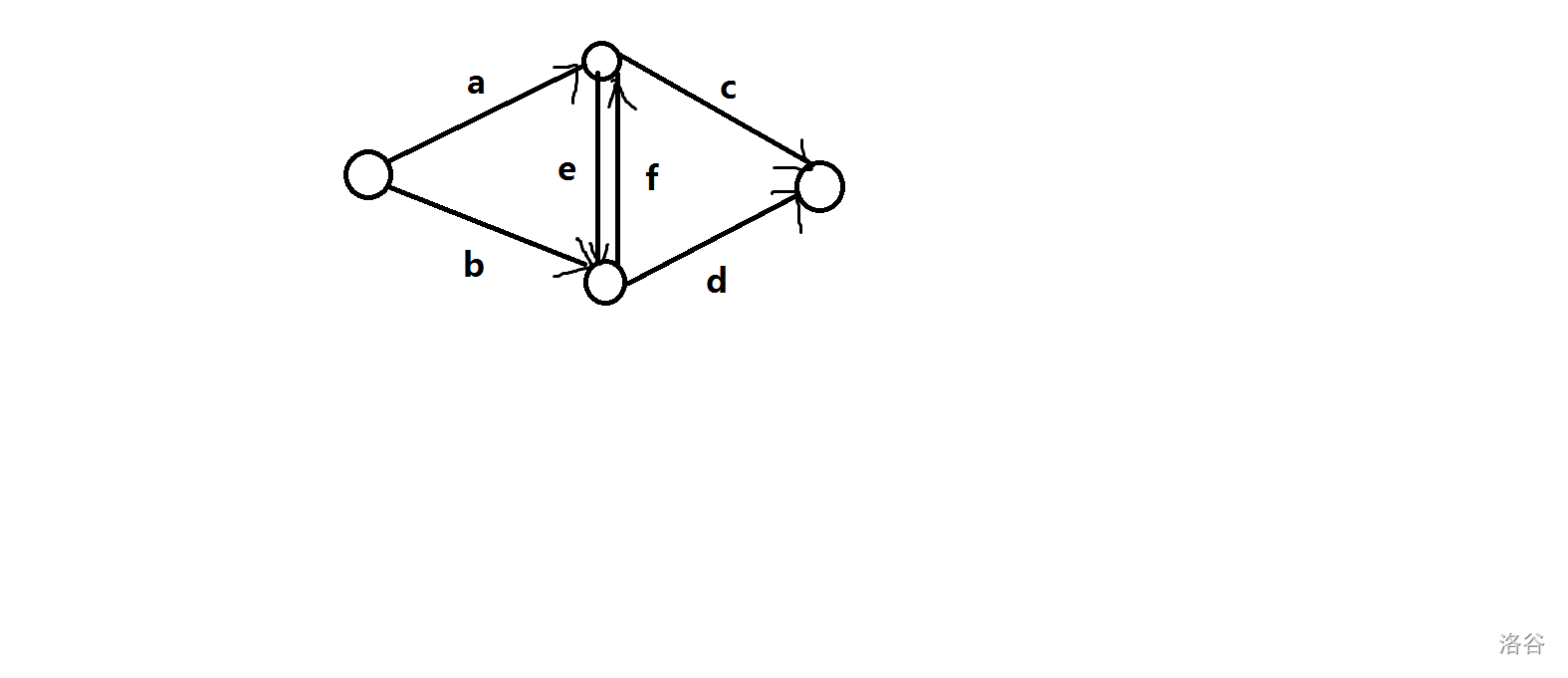
上面的点为 \(i\)，下面的点为 \(j\)，左边选文，右边选理
先设 \(a_i\) 表示 \(i\) 选文科的价值，\(b_i\) 表示 \(i\) 选理科的价值，\(c_{i,j}\) 表示 \(i,j\) 同选文科的价值，\(d_{i,j}\) 表示 \(i,j\) 同选理科的价值。
然后枚举所有的最小割
第一种情况同时选文科，最小割为 \(c,d\) 边权之和，此时需要将 \(c,d\) 选理科的贡献减掉
就有 \(c+d=b_i+b_j+d_{i,j}\)
第二种情况同时选理科，最小割为 \(a,b\) 边权之和
就有 \(a+b=a_i+a_j+c_{i,j}\)
第三种情况 \(i\) 选文科，\(j\) 选理科，最小割为 \(b,c,e\)
