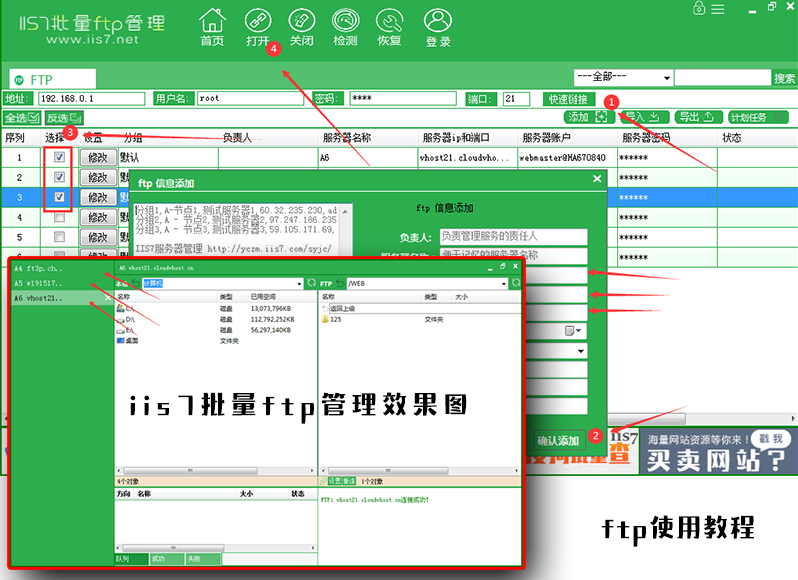
IIS7批量FTP管理功能说明:
1、可批量导入,导出FTP信息
2、其他ftp工具有的功能,我们也有
3、特色功能:可以定时上传下载
4、数据信息列表化、一眼就能知道那个是那个
5、批量连接标签页式切换方便快捷
6、7大连接模式更多好的兼容
7、内嵌编辑器有效解决普通txt记事本乱码
8、锁屏功能当程序有规定时间内没人操作,则自动锁程序。输入密码才可以正常操作
本产品适用于:懒得记录FTP信息和有批量定时备份,上传下载的运维或站长。
图片:
FFT是DFT的高效算法,能够将时域信号转化到频域上,下面记录下一段用python实现的FFT代码。
# encoding=utf-8
import numpy as np
import pylab as pl # 导入和matplotlib同时安装的作图库pylab
sampling_rate = 8000 # 采样频率8000Hz
fft_size = 512 # 采样点512,就是说以8000Hz的速度采512个点,我们获得的数据只有这512个点的对应时刻和此时的信号值。
t = np.linspace(0, 1, sampling_rate) # 截取一段时间,截取是任意的,这里取了0~1秒的一段时间。
x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t) # 输入信号序列,人工生成了一段信号序列,范围在0~1秒
xs = x[:fft_size] # 由上所述,我们只采样了512个点,所以我们只获得了前512个点的数据
xf = np.fft.rfft(xs)/fft_size # 调用np.fft的函数rfft(用于实值信号fft),产生长度为fft_size/2+1的一个复数向量,分别表示从0Hz~4000Hz的部分,这里之所以是4000Hz是因为Nyquist定理,采样频率8000Hz,则能恢复带宽为4000Hz的信号。最后/fft_size是为了正确显示波形能量
freqs = np.linspace(0, sampling_rate//2, fft_size//2 + 1) # 由上可知,我们得到了数据,现在产生0~4000Hz的频率向量,方便作图
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e1000)) # 防止幅值为0,先利用clip剪裁幅度,再化成分贝
pl.figure(figsize=(8, 4)) # 生成画布
pl.subplot(211) # 生成子图,211的意思是将画布分成两行一列,自己居上面。
pl.plot(t[:fft_size], xs) # 对真实波形绘图
pl.xlabel(u"time(s)")
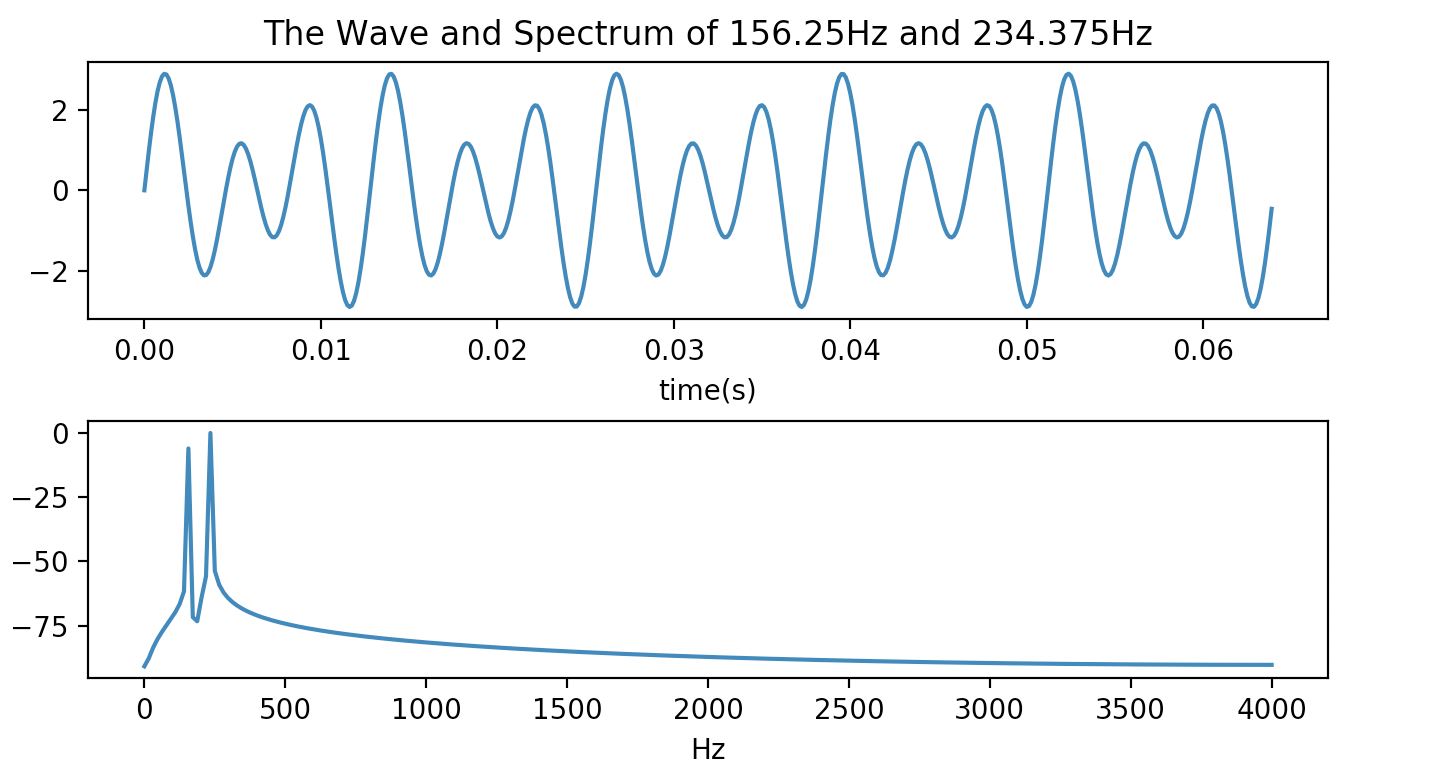
pl.title(u"The Wave and Spectrum of 156.25Hz and 234.375Hz")
pl.subplot(212) # 同理
pl.plot(freqs, xfp) # 对频率和幅值作图,xlabel是频率Hz,ylabel是dB
pl.xlabel(u"Hz")
pl.subplots_adjust(hspace=0.4) # 调节绘图参数
pl.show()
代码进行了详细标注。有一个小细节是FFT对于取样时间有要求。N点FFT进行精确频谱分析的要求是N个取样点包含整数个取样对象的波形。因此N点FFT能够完美计算频谱,对取样对象的要求是n*Fs/N(n*采样频率/FFT长度)在本例中Fs = 8000Hz,N=512 base_freq=15.625Hz 所以本例中给出了频率为156.25Hz(n=10)和234.375Hz(n=15)做例子。
效果如下:
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持IIS7站长之家。